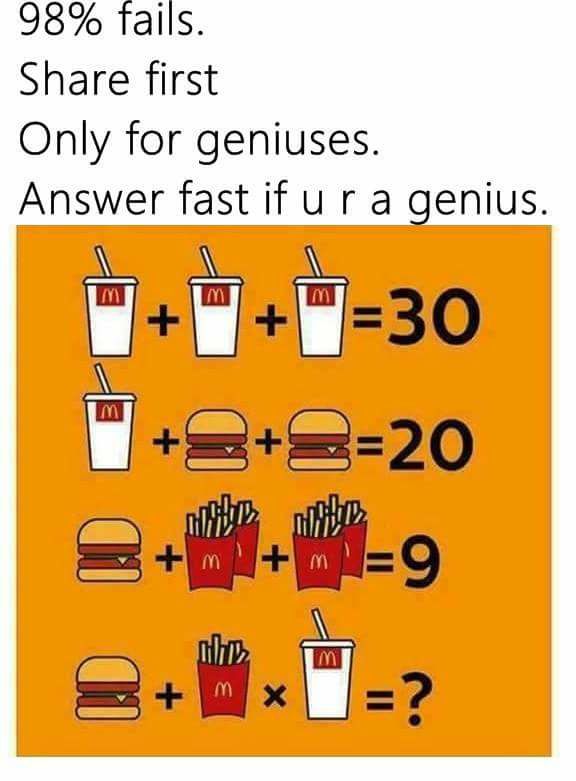On the Mathematics of Fast Food
Social media is the worst. Every time I log on to Facebook, I'm inundated with half-baked political arguments and advertising masquerading as memes. The latest one is totally not an advertisement for McDonald's. It claims that 98% of people cannot solve a certain math problem. Solving these problems is easy if you have the right tools. The problem is: Most people simply did not learn what that is. And that tool is called linear algebra.
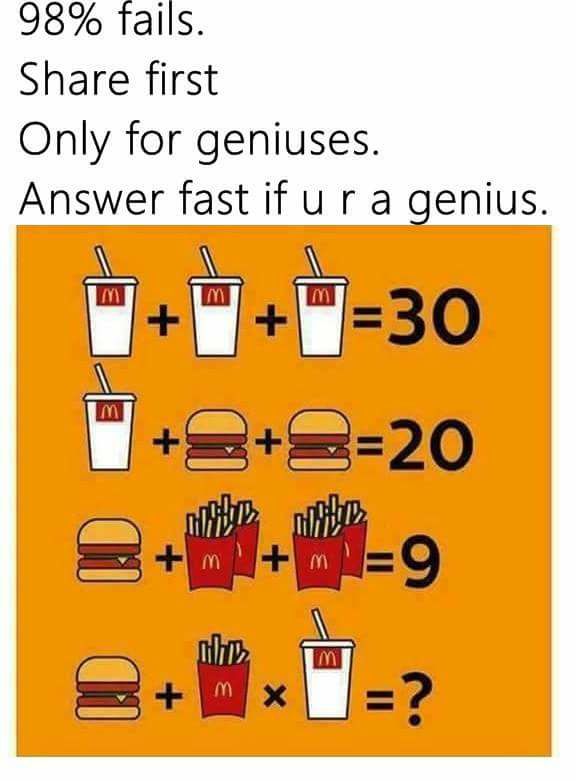
The first thing we have to do is get past how stupid the phrase "u r a genius" looks capture the essence of the system. What really matters here is the first 3 lines describing the relationship of soft drinks, hamburgers, and fries to some unitless numeric value which I assume is associated to some Satanic ritual. It isn't dollars, as it is pretty obvious that hamburgers would cost less than soft drinks, which doesn't make any sense. Satan BitCoins work differently than currencies we're used to.
\(3\,\text{soft drinks}\rightarrow 30\)
\(1\,\text{soft drink} + 2\,\text{hamburgers} \rightarrow 20\)
\(1\,\text{hamburger} + 2\,\text{fries}\rightarrow 9\)
For ease of communication, let's call "soft drinks" \(x\), "hamburgers" \(y\) and "fries" \(z\). We can write our system as a set of 3 simple addition problems.
\(\begin{array}{ccccc}
3x\\
1x & + & 2y\\
& & 1y & + & 2z
\end{array}
\begin{array}{c}=30\\=20\\=9\end{array}\)
The non-presence of \(y\) and \(z\) in the first equation implies the numbers next to the letters is \(0\). Let's write it out just for consistency.
\(\begin{array}{ccccc}
3x & + & 0y & + & 0z\\
1x & + & 2y & + & 0z\\
0x & + & 1y & + & 2z
\end{array}
\begin{array}{c}=30\\=20\\=9\end{array}\)
In math, we like to be concise. The system of equations above has way too much redundancy. We'll factor out \(x\), \(y\), and \(z\) into a column vector and give it the totally-not-confusing name \(\vec{x}\), leaving us with just the numbers in \(\mathbf{A}\). Let's do the same thing with the "answer" numbers and call it \(\vec{b}\). Now we rewrite the whole system into some matrix multiplication. Don't worry -- it's definitely the same thing as above.
\(\underset{\mathbf{A}}{\underbrace{
\begin{pmatrix}3 & 0 & 0\\
1 & 2 & 0\\
0 & 1 & 2
\end{pmatrix}}}
\underset{\vec{x}}{\underbrace{\begin{pmatrix}x\\y\\z\end{pmatrix}}} =
\underset{\vec{b}}{\underbrace{\begin{pmatrix}30\\20\\9\end{pmatrix}}}
\)
The key to all this manipulation is to be able to write this system of equations as a simple one: \(\mathbf{A}\vec{x}=\vec{b}\). Remember, what we're really looking for is \(\vec{x}\) (the values for \(x\), \(y\), and \(z\)), which mathematicians usually write as \(\vec{x}=?\). To do this, we need some manner of getting \(\vec{x}\) by itself, which involves manipulating \(\mathbf{A}\) in some way. That way is the reciprocal, which is the value you multiply a number by to get \(1\). For example, the reciprocal of \(5\) is \(\frac{1}{5}\), which can also be written as \(5^{-1}\). For matrices, we also have reciprocals, but the result of \(\mathbf{A}\mathbf{A}^{-1}\) is usually called \(\mathbf{I}\) instead of just \(1\) (unfortunately, \(\mathbf{1}\) was already taken). In any case, \(\mathbf{I}\) means the same thing as \(1\): Multiplying a matrix with \(\mathbf{I}\) gives you back the same matrix. Let's manipulate our equation to figure out what the hell \(\vec{x}\) is.
\(\mathbf{A}\vec{x}=\vec{b}\)
\(\mathbf{A}{-1}\mathbf{A}\vec{x}=\mathbf{A}{-1} \vec{b}\)
\(\mathbf{I}\vec{x}=\mathbf{A}^{-1} \vec{b}\)
Now all we need is some value for \(\mathbf{A}^{-1}\). The mechanism for discovering this value involves the rote memorization of a boring algorithm. Instead of taking the time to learn the technique, let's just ask Wolfram|Alpha, which happily tells us the answer.
\(\mathbf{A}^{-1} = \frac{1}{12}\begin{pmatrix}4 & 0 & 0\\-2 & 6 & 0\\1 & -3 & 6\end{pmatrix}\)
I have no idea what the meaning of \(\mathbf{A}^{-1}\) is. All I know is that if I multiply \(\mathbf{A}^{-1}\) by \(\mathbf{A}\), I will get \(\mathbf{I}\).
So: What's the correct answer to the original problem?
Who cares? Go outside and have fun. Stop trying to prove your intellect to other people over the internet.
Just use Wolfram|Alpha to find the value of \(\vec{x}\).
\(\vec{x}=\begin{pmatrix}10\\5\\2\end{pmatrix}\)
The result is the associated numeric value for soft drinks (\(x=10\)), hamburgers (\(y=5\)), and fries (\(z=2\)). Since we have numbers, a solution probably exists (if you can figure out how to solve \(y + x \times z\) for known values of \(x\), \(y\), and \(z\)).
Seem cool? Probably not. This problem is mathematically uninteresting, but there are plenty of interesting problems in the world of math! The important takeaway here is knowing math does not make someone more or less intelligent. All it means is they know how to perform some process and speak the appropriate jargon. Linear algebra was not taught at schools until very recently and usually only in "higher-level" math courses, so not knowing how to approach things like this is perfectly normal.
And don't make fun of people who answer with the value of \((y+x) \times z\). Order of operations is a byproduct of representation which is completely irrelevant in the day-to-day life of \(99.999\%\) of people. Stop being an elitist cunt because you can remember something that someone else can't. Remembering doesn't make you special. Nothing makes you special. All you are is food that hasn't died. Or maybe just dust in the wind. I don't know your life.